Amateur Radio (G3TXQ) - Folded dipoles
A. Introduction
A recent interest in "bent" half-wave dipoles led me to look into the theory of the classic Folded Dipole (FD) in some depth. Dipoles bent into a square shape - for example those used in the CobWebb Antenna design - typically exhibit a low feedpoint impedance of around 12Ω and it is convenient to use the impedance transformation characteristics of the FD to improve the VSWR. What I learnt is that the explanation often given in textbooks as to how FDs function is a gross simplification of what is really happening.
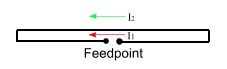
The top drawing on the right is typical of the those you will find in a simple description of a FD. The accompanying text usually asserts that, if the two wires are the same diameter, at resonance the current in the upper wire(I2) and the current in the lower (driven) wire (I1) are the same magnitude and phase at all points along the antenna. Therefore, the feedpoint impedance must have been raised by a factor of 4, because for the same power radiated by a conventional dipole the current has been halved. The assumed current distributions are shown in the second diagram - two sinusoids of equal amplitude and phase.
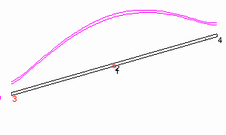
However, when we model a FD in EZNEC we see a subtly different shape to the current distribution as shown in the third diagram. At the centre of the antenna the current follows the sinusoidal shape we would expect, and if we examine the phases of the currents in the upper and lower wires we find they are the same. However, the current does not fall to zero at the ends of the antenna - the distribution has "flattened" - and when we look at the phases of these end currents in the upper and lower wires we find they are the are in anti-phase with one another and in quadrature with the current source at the centre.
There is simple explanation. By adding the upper wire and the end shorting links to form the FD, we have additionally created two short-circuit transmission-line stubs. These stubs - formed by the right hand and left hand sides of the antenna - are close to a quarter-wave in length. Their open ends are at the centre of the FD and the stub short-circuits are the FD shorting links. The two stubs are in series with one another and in parallel with the FD feedpoint. The fourth diagram shows the current distribution attributable to the stubs; it is a maximum at the ends and falls according to a cosine law as we move towards the middle of the FD. The stub currents in the upper and lower wires are in anti-phase because this is a "transmission-line" mode.
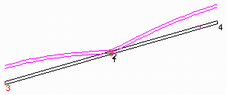
So, the current at any point along the FD is the superposition of two currents: the "antenna-mode" or "common-mode" current which is maximum at the centre of the antenna and which is responsible for the radiation; and the "stub-mode" or "differential-mode" current which is maximum at the ends of the antenna and which does not cause radiation.
Interestingly, early versions of the ARRL Antenna Book have a section on FDs which recognises the stub-effect, but the latest (21st Edition) does not mention it.
We can check the validity of this argument fairly easily by examining the currents in the EZNEC model. With a 1A current source we find that the current flowing in the shorting links is 0.23A. If we are right that this is stub-mode current, it will fall according to the relationship 0.23*cos(θ) as we move towards the middle of the FD. At the same time the "antenna-mode" current will rise from zero according to the relationship 1*sin(θ). At some point the two currents will be equal and, because they are in phase quadrature, the net current will have a phase angle of 45°
Equal magnitude currents occur at distance θ from the ends.
So: 0.23*cos(θ) = 1*sin(&theta)
Giving θ = tan-1(0.23) = 13°
At this point, net current = 1.414*sin(θ) = 0.318A at a phase angle of 45°
If we now check this prediction against the net currents predicted in the EZNEC model we find that the current in the segment nearest to the 13° position is 0.33A at a phase angle of 46.9° - sufficiently close to support the "stub hypothesis".
B. Implications
By using the multiple-source capability of EZNEC it is possible to separate out the antenna-mode characteristics from the stub-mode characteristics, and thereby get a better understanding of the implications for antenna design. Our primary concern is to know what difference the two stubs will make to the tuning and the bandwidth of the antenna. The model used for the following discussion was a 34ft dipole constructed from #14 copper wire with the upper and lower wires separated by 6".
i) Tuning
The antenna-mode resonance for the antenna occurs at 13.72MHz, where the feedpoint impedance is [288+j0] Ohms. This implies a length formula of l = 466/f which is reasonably close to the ARRL Antenna Book formula of l = 468/f.
The stub-mode quarter-wave resonance for this wire gauge and spacing occurs at 14.35MHz, implying a formula of l = Vf * 493 / f if we assume a Velocity Factor of 0.99. Again, this is close to the ARRL Antenna Book formula of l = Vf * 492 / f.
Because 17ft stubs are shorter than a quarter-wave they are inductive at +j9000, and this modifies the antenna-mode impedance slightly at 13.72MHz such that the net FD impedance is [289+j5.7]. Consequently the FD becomes resonant at a marginally lower frequency - 13.70MHz - where the antenna-mode impedance is slightly capacitive and offsets the parallel inductance of the stubs.
Note that an antenna whose stub Velocity Factor is 0.95 will not be de-tuned in any way because the antenna-mode length is identical to the stub-mode length; the stub will be exactly a quarter wave long and its shunting effect on the feedpoint impedance will be minimal.
The reverse happens when the stub Velocity Factor is just below 0.95. The stub is longer than a quarter-wave at the antenna-mode resonant frequency and therefore capacitive. This forces the FD resonance to rise to a frequency where the inductance of the antenna-mode impedance offsets the stub capacitance.
A major problem arises when the stub Velocity Factor is significantly below 0.95 as might be the case if the FD is constructed from 300Ω ribbon or even twin-flex. There are two exacerbating effects:
- The drop in characteristic impedance (which often accompanies the reduced Velocity Factor) reduces the stub reactance and makes its shunting effect more pronounced
- The increased stub length results in a shunting reactance so low that there is no frequency where it can be offset by the reactive component of the antenna-mode impedance.
Fortunately, there is a neat solution to the problem. By moving the shorting links in from the end of the FD to a point where the stubs become a quarter-wavelength, we will make their shunting effect negligible without any significant impact on the antenna-mode characteristics.
In summary: stub Velocity Factors above 0.95 will cause the FD resonant frequency to reduce slightly, and Velocity Factors below 0.95 will cause it to increase, by amounts which also depend on the stub characteristic impedance. In these cases, small adjustments to the overall length of the antenna should be sufficient to tune it successfully. However, a combination of low Velocity Factor and low characteristic impedance (e.g. Vf=0.7 and Zo=100) may make it impossible to find a resonant frequency; in these cases the end shorting links should be moved towards the centre of the antenna, to a point where the stub is a quarter wavelength. The formulae given in the ARRL Antenna Book form a useful starting point:
Antenna length(ft) = 468 / f(MHz)
Shorting link spacing(ft) = Vf * 492 / f(MHz) [for Vf<<0.95]
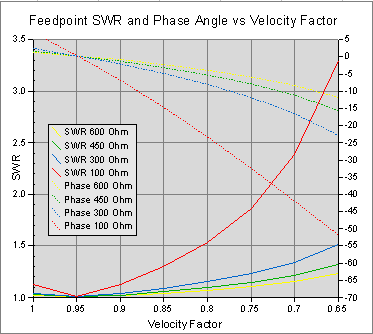
The first chart on the right shows, for a range of Characteristic Impedances and Velocity Factors, what happens to the feedpoint impedance SWR (left Y axis) and phase angle (right Y axis) if we don't move the shorting links inwards. Note:
- At a Velocity Factor of around 0.95 there is no impact on feedpoint impedance, no matter what the Characteristic Impedance;
- Wire having a Characteristic Impedance of 300Ω or higher, with a Velocity Factor of 0.85 or higher, has only a minor impact.
- Wire with a Characteristic Impedance of 100Ω or lower, with a Velocity Factor of 0.88 or lower, probably should not be used without moving the shorting links inwards.
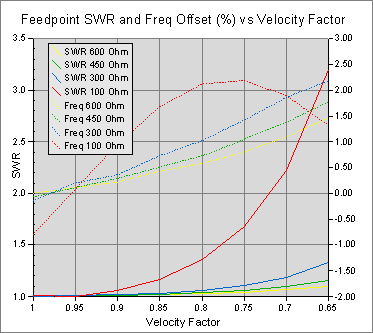
The second chart on the right shows, for a range of Characteristic Impedances and Velocity Factors, what happens if instead of moving the shorting links inwards we compensate by shifting frequency. The chart shows the minimum SWR achievable (left Y axis) and the frequency offset required as a percentage (right Y axis). Note:
- At Velocity Factors close to unity, the resonant frequency falls slightly. This is because the stub is less than a quarter-wave long and therefore inductive. The fall in frequency introduces a compensating capacitive component to the common-mode impedance.
- At Velocity Factors below 0.95, the resonant frequency rises. The stub is longer than a quarter-wave and therefore capacitive. The rise in frequency introduces a compensating inductive component into the antenna common-mode impedance
- At Velocity Factors around 0.95 there is no frequency detuning and no impact on feedpoint impedance, whatever the Characteristic Impedance;
- Wire having a Characteristic Impedance of 300Ω or higher, with a Velocity Factor of 0.85 or higher, has only a minor impact on feedpoint impedance, although minimum SWR occurs as much as 0.75% higher in frequency.
- Wire with a Characteristic Impedance of 100Ω or lower, and with a Velocity Factor of 0.8 or lower, has an unacceptable minimum SWR and it is impossible to find any frequency where the antenna is resonant.
ii) Bandwidth
Most descriptions of the FD claim that it has a wider VSWR bandwidth than a single-wire dipole. Mostly no explanation is given as to why. If an explanation is given, it is usually attributed to the "stub effect" producing offsetting reactance as the frequency is moved away from resonance; the modelling results tell a different story!
A 34ft dipole comprising a single #14 gauge wire has a VSWR bandwidth (ref 73Ω) of 950KHz. The 34ft FD constructed with two #14 gauge wires spaced by 6" has a VSWR bandwidth (ref 288Ω) of 1380KHz. So the FD certainly has extended the VSWR bandwidth by a significant 45%.
However, if we examine the "antenna-mode" of the FD (i.e. ignoring the stubs) we find that it has a VSWR bandwidth of 1340KHz. In other words, 97% of the bandwidth enhancement can be attributed to the increased width of the radiating element, and only 3% to any stub effect. We could achieve close to the same bandwidth enhancement by constructing a conventional dipole with "legs" comprising two wires spaced by 6" in the manner of a classic "cage dipole".
C. Practical experiments
To check out some of this theory I constructed a conventional dipole and a FD using twin power lead which I measured to have a characteristic impedance of 105Ω and a Velocity Factor of 0.66.
I used two lengths of the twin-lead to form a conventional dipole, twisting the four ends together. I trimmed it for resonance at 43 MHz - each leg needed to be 64.25", which suggests a shortening of 1.6% due to the insulation. Its impedance at resonance was 53Ω. Without changing any lengths I reconfigured it as a folded dipole. The feedpoint impedance at 43 MHz was measured as [120-j79] rather than the [212+j0] which would be expected from a simple 4:1 impedance transformation.
This is close to the value we would predict by including the "stub effect". The twin-lead I used has characteristics very close to those of the "ZIP105" line option in one of the on-line transmission line loss calculators; that calculator predicted an input impedance of [17.7-j134.5] for a 64.25" short-circuit stub of this wire. Two such stubs in series, connected across the expected antenna-mode impedance of 212 Ohms (4*53), produces a value of [129-j90].
I calculated that I would need to place a shorting link 45" either side of the centre in order to make the stubs a quarter-wavelength. I put the links in place and the feedpoint then measured 195+j0 - pleasingly close to the expected 212+j0.
Within the limits of my measurement accuracy this seems to support fully the "stub effect" hypothesis and clearly demonstrates the need for inboard shorting links if Vf and Zo are low.